The basic building blocks of fish bodies are proteins. Proteins have structure at several levels. The primary structure is determined by a sequence of the component amino acids, themselves with a structure determined by their sequence of atoms of carbon, hydrogen, etc. The secondary structure of most protein is a primary coil, similar to a braid. A third-level structure can emerge when the braids fold onto themselves, with various loops weakly connected by hydrogen bonds. It is this tertiary structure which determines the external shape of a protein, e.g., of an enzyme and hence how it will lock into 'receptors', often other molecules on the surface of cells.
Thermal noise is ubiquitous above absolute zero (0 Kelvin) and one of its effects is to destroy the tertiary structure of protein, thus rendering it ineffective. As a result, animals must break down such denatured molecules into their constituent parts and re-synthesize them. This is the reason why it costs energy to maintain a living body, even when it 'does' nothing, nor grows. In mammals and birds, which maintain more or less constant internal body temperatures, the enzyme systems are geared such that the rate of synthesis matches a certain level of thermal noise, i.e., that which occurs at 37 to 38°C. In fish, which except for large scombroids and some large sharks, cannot maintain a constant body temperature, different external temperatures thus imply different levels of thermal noise and hence rates of protein denaturation. Thus, metabolic rate must vary with temperature and it does so essentially as a function of the need to re-synthesize protein.
However, it must be understood that the oxygen consumed by a fish is not its oxygen demand but the oxygen supplied to it via its gills, i.e., the fish would use more oxygen if it could get it. Hence, the amount of oxygen consumed by a fish is an imperfect measure of its real 'need' for oxygen. Gill size grows in proportion to a power of body weight that is less than one, i.e., the bigger the fish of a given species become, the smaller the gill area per body weight becomes. Hence, big fish, given a certain level of activity, will tend to run out of oxygen faster than small fish of the same species, other things being equal.
Table 5.1. Ten species in FishBase with growth parameters, at least one length-weight relationship and three records each of gill area and oxygen consumption per unit body weight.

• Choose a species from Table 5.1. Estimate for that species the exponent of a log-log relationship between gill area and body weight, and between oxygen consumption and body weight, and plug into this equation the value for the maximum size reported for that fish in a given habitat. [Hint: maximum lengths by locality are found using the Max. size & age link in the Species Summary page.]
• Compute the gill area per unit weight and oxygen consumption per unit weight at which the fish stops growing. [Hint: Lmax and L∞ may have something to do with this.]
The brain size per body weight of adult animals is related to the sensory and behavioral capabilities of the species to which they belong. For example, fishes with well-developed electrosensing capabilities are known to have large brains. On the other hand, the brain is the body organ with the highest energy and oxygen demand, and thus, fishes as well as other animals have evolved brain sizes that are neither too small nor too large respective to the niches they occupy in nature. [Note as an aside that it is not true that people (at least most) use only 10% of their brain's capacity].
• Based on your general knowledge about the fish and their habitat, rank the following groups according to their brain size: coral reef fish, deep sea fish, herrings, sharks, coelacanths. Explain in a few sentences why you ranked each group as you did.
• For the groups listed above, find typical examples, look at their brain size compared to other fishes, and use these data to test your hypothesis about their respective groups. [Hint: common names often contain parts of a group's scientific name.]
One main brain activity of most vertebrates is the processing of sensory, mainly visual, information. Sleep may have evolved as a response to the need to refresh memory circuits (Kavaneau 1998). This is consistent with the fact that genetically blind fishes that live in caves do not need sleep because their need for processing of sensory information is almost nil (Kavaneau 1998). [For other potential non-sleeping fish species see Kavaneau (1998).]
• Find from FishBase 30 blind fish species. From the Species Summary page extract information related to Habitat and Diet (More Information link) and check their colouration from the available photos. Construct a table with these parameters, draw conclusions and write an essay.
Fishes produce different types of sounds (e.g., grunts, escape sounds, chewing sounds), both actively and passively, under different cases (i.e., when alarmed, when netted, intraspecific competition, territorial behaviour, mating). The main sound production organs are the swim bladder and the teeth, mainly the pharyngeal ones. FishBase (Information by topic, Physiology/Behaviour, Fish sounds) lists the species that produce sound together with accompanying information (i.e., type of sound produced, sound production organ, sonic mechanism, behavioural context, reference and remarks).
• Select 50 sound-producing species and prepare a table listing the types of produced sound, the sound production organ, the sonic mechanism and the behavioural context. Summarise the results in the form of a short essay.
Like other heterotrophic organisms, fish need food to survive and grow. Within ecosystems, trophic (feeding) relationships and energy flows largely define the function of various species. There are two ways of presenting species-specific consumption:
• At the individual level, i.e., as the consumption of a particular food type by a fish of a certain size, in the form of a daily ration (Rd); or
• At the population level, i.e., as the consumption (Q) by an age-structured population of weight (B), in the form of population-weighted consumption per unit biomass (Q/B).
There are a number of methods that can be used to estimate the daily ration of fish: studying the changes in stomach content in the course of a day, direct observation of captive fish, etc. One of these techniques is to infer ration from daily oxygen consumption, which is justified since the oxygen consumed is ultimately combined with the food consumed to generate ATP (adenosine triphosphate, the substance used to fuel internal metabolism). This is illustrated through an example for red piranha, Pygocentrus nattereri, adapted from Pauly (1994):
Data were analyzed using a multiple (log) linear regression which yielded, for prediction of the metabolic rate (C, in mgO2h-1) in small Pygocentrus nattereri, the model:
C =0.387·W 0.539·O21.13 … 5.1)
where W is the live weight of the fish in g, and O2 is the oxygen content of the water, in mg 1-1. The overall fit is good (R=0.950); the standard errors of the exponents are 0.163 and 0.205, respectively, for 4 degrees of freedom. Given the small range of weights considered here, the relatively large standard errors about the estimates, and the low number of degrees of freedom, it would not be appropriate to assume that the slope linking O2 consumption and body weight is, in P. nattereri, significantly different from that proposed by Winberg (1960) for most fishes larger than guppies, i.e., 0.7-0.8. This implies that the equation above can be used only for a small range of weights, here 20 to 160 g.
For a 100 g fish in water with 6 mg O21-1, the equation above predicts an O2 consumption of 35 mg·h-1, i.e., 841 mgO2·day-1. An estimate of daily energy consumption (Q) can be obtained from this using the approach of Wakeman et al. (1979), wherein:
Rd=( ΔW + RESP )/0.75 … 5.2)
where Rd is the daily ration, i.e., daily energy consumption in kcal, ΔW the energy content of the (daily) growth increment, and RESP is the oxygen consumption. The first derivative (i.e., growth rate) of the von Bertalanffy equation in terms of wet weight is:
dW/dt =3KW((W∞/W)1/b-1) … 5.3)
This, solved for W∞=756 g, K=0.893/365=0.00245 day-1, and b =3, gives for a 100 g fish a daily growth increment of 0.706 g, corresponding to 0.706 kcal if the calorific value of fish wet weight is set equal to unity (Brett and Blackburn 1978). The available information on body composition of red piranha flesh (Junk 1976, in Smith 1979) is 8.2 % fat, 15.0 % protein, and 4.4 % ash, not very different from values reported from other fishes (Bykov 1983). Thus, if an oxycaloric equivalent of 0.00325 kcal·mg-1 O2 is assumed, as in other fishes (Elliot and Davidson 1975), the above estimate of 841 mg O2 day-1 becomes 2.733 kcal day-1. Thus:
Rd =(0.706 + 2.733)/0.75 … 5.4)
or 4.585 kcal day-1 for a 100 g piranha. Food conversion efficiency (K1=(dW/dt)/Rd; Ivlev 1966) would then be K1=0.154.
• Compute for species in Table 5.1, the gill area per unit weight and oxygen consumption used only for maintenance. [Hint: fish cease growing when they approach W∞ and conversion between total and fork length can be done from a picture or using the link L-L relationship in the 'More Information' link in the Species Summary page.]
The method outlined above to deal with the ration of fishes led to point estimates, pertaining to a single size or age (group). A fish population consists, however, of different size (age) groups, with small sizes and ages being far more abundant than large sizes and ages. Thus, drawing inferences from one (or several) ration estimate(s) pertaining to a given size (range) of fish, to a population containing a multitude of size groups, requires a knowledge of the size (age) structure of the population. An approach for performing this inference is given in FishBase.
A large number of such inferences, from ration to population weighted food consumption estimates (Q/B), have been performed in recent years, notably Palomares and Pauly (1998). These estimates of Q/B can be used in the context of empirical models to predict Q/B from other, easy-to-estimate parameters. One such equation is:
log10Q/B=7.964-0.204logW∞-1.965T'+0.083A+0.532h+0.398d … 5.5)
where Q/B is the food consumption, W∞ is the asymptotic weight in grams, T'=1000/(°C+273), A is the aspect ratio of the caudal fin= h2/s, h=1 and d=0 for herbivores, h=0 and d=1 for detritivores, and h=0 and d=0 for carnivores.
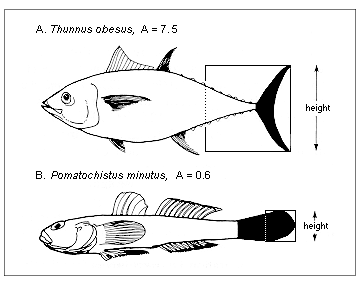
Figure 5.1. Aspect ratio (A) of the caudal fin (see section 3.3 on Diversity of shapes)
Here, one key input is the aspect ratio of the caudal fin defined as in Figure 5.1. Fish with tails with high aspect ratio consume more food than fish with low aspect ratio tails, other things being equal. Needless to say, equation (5.5) cannot be used for fish (e.g., eels) which do not use their caudal fin as their main propulsive organ. Other approaches can be used in such cases.
• Identify through FishBase, pictures of three species of fish covering a wide range of caudal fin aspect ratio: one with an aspect ratio of around 1; one with an aspect ratio of around 3-4, and one with an aspect ratio of above 7. [Hint: using a square grid on a transparency and counting the number of square units or cells occupied by the caudal fin to estimate the fin area should help.]
• Use the aspect ratio, the body size, and the temperature of the habitat to infer Q/B given equation (5) above, and (a) a herbivorous diet; or (b) a carnivorous diet. [Hint: the equation is also implemented in the Life-history tool available from the bottom of the Species Summary pages.]