5. Φυσιολογία

       Οι βασικές δομικές μονάδες του σώματος των ψαριών είναι οι πρωτεΐνες. Οι πρωτεΐνες έχουν πολυεπίπεδη δομή. Η πρωτοταγής δομή τους καθορίζεται από την ακολουθία των αμινοξέων που τις αποτελούν, τα οποία έχουν δομή που καθορίζεται από την ακολουθία των ατόμων άνθρακα, υδρογόνου, κλπ. Η δευτεροταγής δομή των περισσοτέρων πρωτεϊνών είναι μια πρωτογενής έλικα, παρόμοια με μια πλεξούδα. Η τριτοταγής δομή μπορεί να προκύψει από την αναδίπλωση των πλεξούδων μεταξύ τους, με διάφορους βρόγχους που συνδέονται με ασθενείς δεσμούς υδρογόνου. Η τριτοταγής δομή είναι αυτή που καθορίζει την εξωτερική μορφή μιας πρωτεΐνης, π.χ. ενός ενζύμου, και, έτσι, το πώς θα κλειδώσει σε ‘υποδοχείς’, που συχνά είναι άλλα μόρια στην επιφάνεια των κυττάρων.

5.1. Μεταβολισμός, βράγχια και μέγεθος

Ο θερμικός θόρυβος βρίσκεται παντού σε θερμοκρασίες πάνω από το απόλυτο μηδέν (0 Kelvin) και μια από τις επιδράσεις του είναι η καταστροφή της τριτοταγούς δομής μιας πρωτεΐνης, καθιστώντας την έτσι ανενεργή. Έτσι, τα ζώα πρέπει να αποδομήσουν τέτοια μετουσιωμένα μόρια στα συστατικά τους και να τα επανασυνθέσουν. Αυτός είναι ο λόγος για τον οποίο απαιτείται ενέργεια για τη διατήρηση ενός οργανισμού, ακόμα και όταν αυτός δεν ‘κάνει’ τίποτα, ούτε αυξάνει. Στα θηλαστικά και τα πτηνά, τα οποία διατηρούν, περισσότερο ή λιγότερο, σταθερές εσωτερικές θερμοκρασίες σώματος, τα ενζυμικά συστήματα προσαρμόζονται έτσι ώστε ο ρυθμός σύνθεσης να εναρμονίζεται με ένα ορισμένο επίπεδο θερμικού θορύβου, δηλ. αυτό που εμφανίζεται στους 37-38 °C. Στα ψάρια, που εκτός από τα μεγάλα σκομβροειδή και μερικούς μεγάλους καρχαρίες δεν μπορούν να διατηρήσουν  σταθερή θερμοκρασία σώματος, οι διαφορετικές εξωτερικές θερμοκρασίες προκαλούν διαφορετικά επίπεδα θερμικού θορύβου και έτσι διαφορετικούς ρυθμούς πρωτεϊνικής μετουσίωσης. Συνεπώς, ο ρυθμός μεταβολισμού μεταβάλλεται με τη θερμοκρασία με τέτοιο τρόπο ώστε να ακολουθεί την ανάγκη επανασύνθεσης της πρωτεΐνης.

Πρέπει να γίνει κατανοητό ότι η ποσότητα του οξυγόνου που καταναλώνει ένα ψάρι δεν καλύπτει την πραγματική του απαίτηση σε οξυγόνο αλλά το οξυγόνο που μπορεί να αντλήσει μέσα από τα βράγχιά του. Το ψάρι, δηλαδή, θα χρησιμοποιούσε περισσότερο οξυγόνο αν μπορούσε να το αντλήσει από το νερό. Άρα, το ποσό οξυγόνου που καταναλώνει ένα ψάρι είναι μια ατελής εκτίμηση της πραγματικής του ‘ανάγκης’ σε οξυγόνο. Το μέγεθος των βραγχίων αυξάνει εκθετικά με το βάρος σώματος, αλλά ο εκθέτης είναι μικρότερος από τη μονάδα, δηλαδή, όσο μεγαλύτερα είναι τα άτομα ενός είδους, τόσο μικρότερη είναι η επιφάνεια των βραγχίων ανά βάρος σώματος. Έτσι, κάτω από ίδιες συνθήκες, και στο ίδιο επίπεδο δραστηριότητας, τα μεγαλόσωμα άτομα θα έχουν την τάση να ‘ξεμένουν’ από οξυγόνο πιό γρήγορα από ότι τα μικρόσωμα άτομα του ίδιου είδους.

5.1.1. Πίνακας 5.1

Δέκα είδη για τα οποία υπάρχουν διαθέσιμα στοιχεία στη FishBase για τις παραμέτρους αύξησης, τουλάχιστον μια σχέση μήκους-βάρους και τρεις αναφορές για το καθένα για την επιφάνεια των βραγχίων και την κατανάλωση οξυγόνου ανά μονάδα σωματικού βάρους.

5.1.2. Άσκηση 5.1

Εργασία για το φοιτητή

·      Επιλέξτε ένα είδος από τον Πίνακα 5.1. Εκτιμήστε γι’ αυτό το είδος τον εκθέτη της σχέσης ανάμεσα στην επιφάνεια των βραγχίων και το βάρος σώματος (σε λογαριθμική μορφή), και ανάμεσα στην κατανάλωση οξυγόνου και το βάρος σώματος, και εισάγετε στην εξίσωση την τιμή για το μέγιστο μέγεθος που αναφέρεται για το είδος σε μια περιοχή. [Υπόδειξη: τα μέγιστα μήκη του είδους ανά περιοχή βρίσκονται επιλέγοντας Μεγ. μέγεθος & ηλικία (Max. size & age) στη  σελίδα Σύνοψη Είδους (Species Summary).]

·      Υπολογίστε την επιφάνεια των βραγχίων ανά μονάδα βάρους και την κατανάλωση οξυγόνου ανά μονάδα βάρους στην οποία το ψάρι σταματά να αυξάνει.  [Υπόδειξη: Τα L_max και L_¥ μπορεί να σχετίζονται με αυτό.]

Θέματα που σχετίζονται με το μεταβολισμό στη FishBase:

5.2.        Κατανάλωση τροφής

      Όπως και άλλοι ετερότροφοι (heterotrophic) οργανισμοί, τα ψάρια χρειάζονται τροφή για να επιβιώσουν και να αυξηθούν. Μέσα στα οικοσυστήματα, οι τροφικές σχέσεις και οι ενεργειακές ροές καθορίζουν, σε μεγάλο βαθμό, τη λειτουργία των ειδών. Υπάρχουν δυο τρόποι παρουσίασης της κατανάλωσης τροφής ενός είδους:

·    σε ατομικό επίπεδο, δηλ. ως κατανάλωση ενός συγκεκριμένου τύπου τροφής από ένα ψάρι συγκεκριμένου μεγέθους, με τη μορφή σιτηρέσιου (R_d) (ration), ή

·    σε επίπεδο πληθυσμού, δηλ., ως κατανάλωση (Q) από έναν ηλικιακά δομημένο πληθυσμό που έχει συνολική βιομάζα B, με τη μορφή κατανάλωσης ανά μονάδα βιομάζας (Q/B).

Υπάρχουν διάφορες μεθόδοι για τον υπολογισμό του σιτηρέσιου των ψαριών: μελετώντας τις αλλαγές στο στομαχικό περιεχόμενο στη διάρκεια της ημέρας, από την άμεση παρακολούθηση ψαριών σε αιχμαλωσία, κλπ. Μια από τις υπάρχουσες τεχνικές στηρίζεται στον υπολογισμό του σιτηρέσιου από την ημερήσια κατανάλωση οξυγόνου. Αυτό δικαιολογείται από το γεγονός ότι το οξυγόνο που καταναλώνει ένα ψάρι τελικά συνδυάζεται με την ποσότητα της τροφής που καταναλώνεται για να παραχθεί ΑΤΡ (τριφωσφορική αδενοσίνη, η ουσία που χρησιμοποιείται για να τροφοδοτήσει τον εσωτερικό μεταβολισμό). Η μέθοδος αυτή παρουσιάζεται με το παρακάτω παράδειγμα για τα κόκκινα πιράνχας (red piranha), Pygocentrus nattereri, που προσαρμόστηκε από τον Pauly (1994).

Τα δεδομένα (μετά από λογαρίθμηση) αναλύθηκαν με πολλαπλή γραμμική παλινδρόμηση. Το μοντέλο πρόβλεψης του ρυθμού μεταβολισμού (C, σε mgΟ₂ · h^-1) σε μικρά άτομα του είδους Pygocentrus nattereri που προέκυψε περιγράφεται από τη σχέση:

C = 0.387 · W^0.539· O₂^1.13                                             … 5.1)

όπου το W είναι το υγρό βάρος του ψαριού σε g και Ο₂ είναι η συγκέντρωση του οξυγόνου στο νερό, σε mg 1^-1. Η προσαρμογή του μοντέλου ήταν καλή (R = 0.950), και τα τυπικά σφάλματα των εκθετών βρέθηκαν 0,163 και 0,205, αντίστοιχα, για 4 βαθμούς ελευθερίας. Αν ληφθεί υπόψη το μικρό εύρος βαρών που μελετήθηκε, τα σχετικά μεγάλα τυπικά σφάλματα των εκτιμήσεων, και το μικρό αριθμό των βαθμών ελευθερίας, τότε μπορούμε να υποθέσουμε ότι η κλίση που συνδέει την κατανάλωση Ο₂ και το σωματικό βάρος στο P. nattereri δεν διαφέρει σημαντικά από την κλίση που προτείνει ο Winberg (1960), 0.7-0.8, για τα περισσότερα είδη που είναι μεγαλύτερα από τα μικρόσωμα τροπικά είδη της οικογένειας Poeciliidae (guppies). Αυτό δηλώνει ότι η παραπάνω εξίσωση μπορεί να χρησιμοποιηθεί μόνο για ένα μικρό εύρος βαρών (εδώ από 20 ως 160 g).

Για ένα ψάρι 100 g που ζει σε νερό περιεκτικότητας 6 mg O₂1^-1, η παραπάνω εξίσωση προβλέπει κατανάλωση Ο₂ 35 mg·h^-1, δηλ. 841 mg O₂ ·ημέρα ^-1. Μια εκτίμηση της ημερήσιας κατανάλωσης ενέργειας (Q) μπορεί να γίνει από την παραπάνω κατανάλωση οξυγόνου χρησιμοποιώντας την προσέγγιση των Wakeman et al. (1979):

R_d = (DW + RESP)/0.75                                            … 5.2)
 

όπου R_d είναι το σιτηρέσιο, δηλ., η ημερήσια κατανάλωση ενέργειας σε kcal, ΔW το περιεχόμενο σε ενέργεια της (ημερήσιας) αύξησης και RESP είναι η κατανάλωση οξυγόνου.

Το πρώτο παράγωγο (δηλ. ο ρυθμός αύξησης) της εξίσωσης του von Bertalanffy σε υγρό βάρος είναι:

dw/dt = 3KW ((W_¥/W)^1/b-1)                           … 5.3).
 

Η εξίσωση 5.3 αν λυθεί για W_¥ = 756 g, K = 0,893/365 = 0,00245.ημέρα^-1, και b = 3, δίνει για ένα ψάρι που έχει βάρος 100 g μια ημερήσια αύξηση 0,706 g, που αντιστοιχεί σε 0,706 kcal (αν η θερμιδική αξία του υγρού βάρους του ψαριού θεωρηθεί ίση με τη μονάδα: Brett & Blackburn 1978). Οι υπάρχουσες πληροφορίες για τη σύνθεση της σάρκας των κόκκινων πιράνχας (Junk 1976, σε Smith 1979) είναι 8,2% λίπος, 15,0% πρωτεΐνη και 4,4% τέφρα (ash). Οι τιμές αυτές δεν διαφέρουν πολύ από τις τιμές που αναφέρονται για άλλα ψάρια (Bykov 1983). Έτσι, αν θεωρήσουμε ένα οξυγονοθερμιδικό ισοδύναμο ίσο με 0,00325 kcal·mg^-1 O₂, όπως σε άλλα ψάρια (Elliott & Davidson 1975), το παραπάνω αποτέλεσμα των 841 mg Ο₂ ημέρα^-1 γίνεται 2,733 kcal ημέρα^-1. Έτσι, από την εξίσωση 5.2 προκύπτει ότι:

R_d = (0,706 + 2,733)/0,75                                           … 5.4)
 

ή 4,585 kcal ημέρα^-1 για ένα πιράνχας βάρους 100 g. Στην περίπτωση αυτή, η μετατρεψιμότητα της τροφής (K₁ = (dw/dt)/ R_d , Ivlev 1966) είναι Κ₁ = 0,154.

5.2.1. Άσκηση  5.2. 

Εργασία για το φοιτητή:

·      Υπολογίστε για τα είδη του Πίνακα 5.1 την επιφάνεια των βραγχίων ανά μονάδα βάρους και την κατανάλωση οξυγόνου που χρησιμοποιείται μόνο για συντήρηση [Υπόδειξη: τα ψάρια σταματούν να αυξάνουν όταν φτάσουν το W_¥ και η μετατροπή ανάμεσα στο ολικό και το μεσουραίο μήκος μπορεί να γίνει από μία εικόνα του είδους ή από εξισώσεις που υπάρχουν καταχωρημένες για διάφορα είδη στην FishBase.]

Θέματα σχετικά με το σιτηρέσιο που καλύπτονται στη FishBase:

5.3.  Υπολογισμός κατανάλωσης τροφής από εμπειρικά μοντέλα

Η μέθοδος που περιγράφηκε παραπάνω για τo σιτηρέσιο των ψαριών οδηγεί σε εκτιμήσεις που αφορούν μιά συγκεκριμένη κλάση μεγέθους ή ηλικίας. Όμως, ένας πληθυσμός αποτελείται από πολλές κλάσεις μεγεθών (και ηλικιών), με τις μικρές κλάσεις μεγεθών και τις μικρές κλάσεις ηλικιών να υπερτερούν αριθμητικά κατά πολύ των μεγάλων κλάσεων μεγεθών και ηλικιών. Έτσι, η εξαγωγή συμπερασμάτων από ένα ή περισσότερους υπολογισμούς σιτηρεσίων που αφορούν ένα συγκεκριμένο μέγεθος (ή εύρος μεγεθών) ψαριών για όλο τον πληθυσμό, που περιέχει πολλές κλάσεις μεγεθών, απαιτεί τη γνώση της δομής του πληθυσμού σε σχέση με το μέγεθός (ηλικία) τους. Στη FishBase υπάρχει ένας τρόπος προσέγγισης για να γίνονται τέτοιοι υπολογισμοί.

Τα τελευταία χρόνια, έχουν γίνει εκτιμήσεις του Q/B - από το σιτηρέσιο - για πολλά είδη, κυρίως από τους Palomares & Pauly (1998). Αυτές οι εκτιμήσεις του Q/B μπορούν να χρησιμοποιηθούν στα πλαίσια εμπειρικών εξισώσεων για την πρόβλεψη του Q/B από άλλες, πιο εύκολα υπολογίσιμες παραμέτρους. Μια τέτοια εξίσωση είναι:

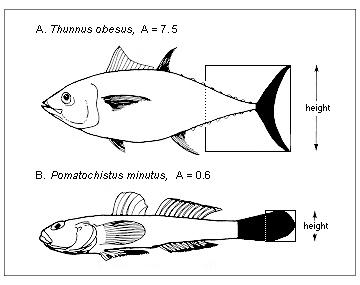
log Q/B = 7.964 – 0.204logW_¥ – 1.965T’ + 0.083A + 0.532h + 0.398d       … 5.5)
 

όπου Q/B είναι η κατανάλωση τροφής, W_¥ είναι το ασυμπτωτικό βάρος σε g, Τ’= 1000/(°C+273), Α είναι η αναλογία όψης του ουραίου πτερυγίου (Α= h²/s, όπου s και h είναι η επιφάνεια και το ύψος του ουραίου πτερυγίου, αντίστοιχα), h=1 και d=0 για τα φυτοφάγα είδη, h=0 και d=1 για τα θρυμματοφάγα είδη και h=0 και d=0 για τα σαρκοφάγα είδη.

Στην εξίσωση 5.5 καθοριστική είναι η αναλογία όψης του ουραίου πτερυγίου, η οποία ορίζεται στην Εικόνα 5.1. Είδη με μεγάλη αναλογία όψης ουραίου πτερυγίου καταναλώνουν περισσότερη τροφή απ’ ότι είδη με μικρή αναλογία όψης ουραίου πτερύγιου, όταν όλες οι υπόλοιπες παράμετροι παραμένουν σταθερές. Βέβαια, είναι φυσικό ότι η εξίσωση 5.5 δεν μπορεί να χρησιμοποιηθεί για είδη (π.χ. χέλια) τα οποία δεν χρησιμοποιούν το ουραίο πτερύγιο ως κύριο μέσο προώθησης. Για τα είδη αυτά, μπορούν να χρησιμοποιηθούν άλλες προσεγγίσεις.

5.3.1.      Εικόνα 5.1. Α αναλογία όψης ουραίου πτερυγίου

5.3.2. Άσκηση 5.3

Εργασία για το φοιτητή:

·      Αναγνωρίστε μέσα από τη FishBase, φωτογραφίες 3 ειδών που να καλύπτουν ένα ευρύ φάσμα αναλογίας όψης ουραίου πτερυγίου: ένα με αναλογία όψης περίπου 1, ένα με αναλογία όψης περίπου 3-4 και ένα με αναλογία όψης μεγαλύτερη από 7. [Υπόδειξη: θα βοηθούσε  η χρήση ενός τετραγωνικού πλέγματος πάνω σε μια διαφάνεια. Μετρώντας τον αριθμό των τετραγώνων που καταλαμβάνει το ουραίο πτερύγιο μπορεί κάποιος να υπολογίσει το εμβαδόν του ουραίου πτερυγίου.]

·      Χρησιμοποιήστε την αναλογία όψης, το μέγεθος του σώματος και τη θερμοκρασία του ενδιαιτήματος για να υπολογίσετε το Q/B από την εξίσωση 5.5 παραπάνω, για (α) ένα φυτοφάγο και (β) ένα σαρκοφάγο είδος. [Υπόδειξη: η εξίσωση 5.5. τίθεται, επίσης, σε εφαρμογή στη σελίδα Εργαλείο ιστορίας ζωής (Life-history tool).]

Θέματα σχετικά με την κατανάλωση τροφής που καλύπτονται στη FishBase: